Tere tulemast Eestisse! Kas olete kunagi mõelnud sellest, kuidas keeruliste probleemide lahendamine võib olla lihtsam kui arvate? “Murruline tuletis murrab läbi keerulistest probleemidest | Teadus 3 minutiga” on põnev teema, mis viib teid teadusmaailma sügavustesse vaid mõne minutiga. See lühike, kuid haarav loeng avab uksed matemaatilise mõtlemise ja probleemide lahendamise uutele viisidele. Olles Eestis, on teil võimalus avastada teaduse võlusid ning õppida midagi uut ja põnevat. Ärge laske võimalust käest ära!
Ehkki matemaatilised funktsioonid on teinud loodusteadlaste elu hulga lihtsamaks, võib muutuda võrrandite lahendamine arvutiprogrammide jaoks ääretult ajamahukaks. Tartu Ülikooli matemaatikute välja töötatud arvutusmeetod aitab paremini lahendada murrulisi tuletisi sisaldavaid võrrandeid, millest võib kasu olla nii meditsiinis, kliimauuringutel kui ka finantsmaailmas.
Elu meie ümber kirjeldavad erinevad funktsioonid. Näiteks saame funktsiooni abil panna kirja, kui pika vahemaa liigub auto igal ajahetkel. Võttes nüüd sellest auto liikumist kirjeldavast funktsioonist tuletise, saame kirjeldada auto liikumise kiirust. Kui võtame omakorda tuletise kiiruse funktsioonist, saame me auto kiiruse muutumise kiiruse ehk kiirenduse, kirjutab Tartu Ülikooli matemaatika nooremteadur Hanna Britt Soots.
Arvutades funktsioonist tuletise, nimetame lõpptulemust funktsiooni esimest järku tuletiseks, võttes funktsioonist tuletist kaks korda, nimetame seda funktsiooni teist järku tuletiseks. Niiviisi jätkates saame arvutada funktsiooni viiendat järku tuletist, sajandat järku tuletist ja minna veel kaugemalegi.
Kas me saame võtta funktsioonist aga ka näiteks ½ järku tuletist ning kui jah, siis mida see tähendab? Seda küsisid juba matemaatikud L’Hospital and Leibniz üksteiselt juba 17. sajandi lõpus, kuid ühest vastust nad ei leidnudki. Kirjavahetuse tõttu hakkasid matemaatikud taolisi tuletisi kutsuma murrulisteks tuletisteks ja need pakkusid teoreetilist huvi mitmele matemaatikule. Populaarsemaks said need aga alles ligi 300 aastat hiljem, sest avastati, et murrulised tuletised on väga kasulikud kirjeldamaks protsesse nii füüsikas, keemias, bioloogias, majanduses kui ka pilditöötluses.
Üks selline valdkond on näiteks erinevad difusiooniprotsessid. Need ulatuvad soojuse levikust materjalides kuni molekulide hajumisena vedelikes, mängides võtmerolli mitmesuguste nähtuste iseloomustamisel. Näiteks saab selle abil kirjeldada nii õhusaastet meie ümber kui ka maksa mürkainete filtreerimistööd meie kehas.
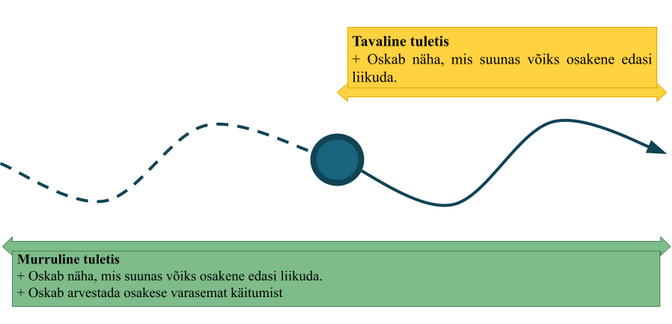
Traditsiooniliselt on difusiooni tõhusalt kirjeldatud klassikaliste täisarvuliste diferentsiaalvõrrandite abil ehk siis kasutades esimest või teist järku tuletisi. Siiski ei suuda need tavalised mudelid edukalt anda ülevaadet protsessides, kus difusiooniprotsess käitub ebatavaliselt. Näiteks kui osakeste vahel toimub keemiline reaktsioon või nende liikumine sõltub nende varasemast käitumisest ehk mälust.
Probleemi lahendamiseks saamegi võtta appi hoopis murrulised tuletised, mis oskavad näha difusiooniprotsessis suuremat pilti ja arvestada difusiooni osakeste varasemat käitumist paremini, kui seda oskab teha tavaline tuletis.
Võrrandite lahendamiseks on tihti vaja arvuteid
Matemaatika abil on võimalik lihtsamad tuletisi sisaldavaid võrrandeid lahendada oma kodus paberi ja pliiatsi abil. Seda nimetame me analüütiliseks lahendamiseks. Näiteks kui meil on diferentsiaalvõrrand:
f’ = f
ehk teame, et funktsiooni f tuletis on võrdne tema endaga, siis on teada, et selliseks funktsiooniks f sobib eksponentfunktsioon f(x) =ex. Seda saame kontrollida, kui võtame nüüd meie leitud funktsioonist f(x) tuletise ja näeme, et see on võrdne eksponentfunktsiooniga.
Sellised lihtsaid võrrandeid näeme aga paraku pigem ülesanneteõpikutes kui päris maailmas. Tihti ei suuda me keerulisimaid võrrandeid paberi ja pliiatsiga üldse lahendada. Takistuse ületamiseks on võimalik analüütilise lahendamise asemel lahendada võrrand hoopis numbrilise meetodiga, kasutades erinevaid arvutiprogramme. Numbrilise lahendamise puhul ei ole tavaliselt esimeseks vastuseks mitte võrrandis peituv funktsioon, vaid funktsiooni ligikaudne väärtus erinevates punktides.
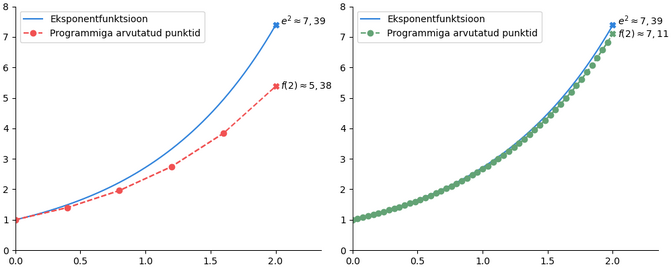
Näiteks võttes selle sama diferentsiaalvõrrandi f’ = f ja üritame seda ühe lühikese arvutiprogrammi abil lahendada, ei saa me enam vastuseks, et tegemist on eksponentfunktsiooniga. Küll aga saame teada, et kui x= 2, siis funktsiooni väärtus on umbkaudu 5,38. Päriselt on eksponentfunktsiooni väärtus x=2 korral umbkaudu 7,39.
Praegu ei tee arvutiprogramm eriti täpset tööd, parema tulemuse saamiseks peame tegema rohkem arvutusi rohkemate punktide korral. Näiteks kui teha juba kümme korda rohkem arvutusi, saame palju täpsema tulemuse: kui x=2, siis funktsiooni väärtus on umbkaudu 7,11.
Ometigi, kui teha liiga palju arvutusi, läheb meie arvutiprogramm liiga aeglaseks. Kui meil on peale selle tekkinud juhuslikult mingi arvutuslik viga, siis see viga võib pika aja jooksul võimenduda ja saadud tulemus ei ole piisavalt täpne. Samuti ei ole meil ühte kindlat arvutiprogramm, mis suudaks lahendada kõiki erinevaid diferentsiaalvõrrandeid, sest me peame enne analüüsima, milline meetod sobib antud matemaatilise võrrandi lahendamiseks
Murruliste tuletiste numbriline lahendamine
Kuna paljude protsesside kirjeldamiseks sobivad murrulised tuletised paremini kui klassikalised tuletised, on sobivate numbriliste meetodite väljatöötamine suureks abiks mitmes erinevas teadusharus. Sobiva meetodi leidmiseks on kõigepealt vaja teada, millistel tingimustel on võimalik üldse diferentsiaalvõrrandile leida sobiv lahend; milline numbriline meetod annab täpsema tulemuse ning kui kiiresti suudab arvutiprogramm leida sobiva lahendi.
Eelmisel aastal uurisin täpsemalt, kuidas on võimalik lahendada neid difusioonivõrrandeid, kus osakeste liikumine on veidi aeglasem, kui seda võiks oodata klassikalise difusioonivõrrandi puhul. Seetõttu on mõistlik osakeste liikumise kirjeldamiseks kasutada murrulisi tuletisi, mitte esimest või teist järku tuletisi. Selgus, et kasulik on luua selline arvutiprogramm, mis teeb rohkem arvutusi süsteemi ajahetke alguspoole kui lõpupoole, sest uuritav difusioonivõrrand muutub rohkem alguspoole.
Sarnaseid difusioonivõrrandeid on uurinud teisedki, aga teatud tingimustel peab minu arvutiprogramm tegema vähem arvutusi, et saada piisavalt täpne lahendus. Loodetavasti on aga saadud tulemused piisavalt kõnekad, et huvi oma teadustöö optimeerimise vastu tekib rohkematel teadlastel. Matemaatikast võib olla kasu ka kohtades, kus me seda esmapilgul oodata ei oskaks.
Artikkel ilmus Eesti Teaduste Akadeemia korraldatava konkursi “Teadus 3 minutiga” raames, mille finaal toimub 2. veebruaril.
Hanna Britt Soots uurib murruliste diferentsiaalvõrrandite omavahelisi seoseid. Oma teadustööga seonduvalt huvitab Sootsi, kuidas on võimalik matemaatikat rakendada teistes teadusharudes. Lisaks doktoritööle õpetab ta gümnaasiumis programmeerimist ning on aktiivne üliõpilasesindaja erinevates ülikooli otsustuskogudes. Vabal ajal tegeleb Soots kudumisega ja naudib briti huumorisarju.
Kokkuvõttes võib öelda, et murruline tuletis võib tõepoolest avada uksi keerulistele probleemidele. See teaduslik lähenemine on oluline mitte ainult teadlastele, vaid ka õpilastele ja üliõpilastele, kes seisavad silmitsi keeruliste matemaatiliste ja teaduslike väljakutsetega. Murrulise tuletise kasutamine võib aidata paremini mõista probleemide olemust ja leida innovaatilisi lahendusi. Seega on oluline jätkuvalt uurida ja arendada murrulise tuletise kontseptsiooni, et aidata kaasa uute avastuste ja edusammude saavutamisele erinevates teadusvaldkondades.

Võib-olla tunnete huvi:
Kõigi riigiteenistujate 35-päevast puhkust seadusesse siiski ei kirjutata | Eesti
Selgus Prantsusmaa jalgpallikoondis koduseks olümpiaks | Jalgpall
Djokovic tagas Wimbledonis koha poolfinaalis | Tennis
Võrklaev soovitas Rail Balticu ettevõtte viia börsile | Majandus
Vene parlament kinnitas maksutõusud | Välismaa
Briti ja Prantsuse valimissüsteemid moonutavad tulemusi stabiilsuse nimel | Ühiskond
EM-i blogi | Kellest saab teine finalist? | Jalgpalli EM
Rein Sikk: igaüks, kes Venemaale läheb, maksku Eestile kümme eurot | Arvamus